AETv2:
AutoEncoding Transformations for Self-Supervised
Representation Learning by Minimizing Geodesic Distances in Lie Groups
 Guo-Jun Qi
Guo-Jun Qi
Laboratory for MAchine Perception and LEarning (MAPLE)
Abstract: Self-supervised learning by predicting transformations has demonstrated outstanding performances in both unsupervised and (semi-)supervised tasks. Among the state-of-the-art methods is the AutoEncoding Transformations (AET) by decoding transformations from the learned representations of original and transformed images. Both deterministic and probabilistic AETs rely on the Euclidean distance to measure the deviation of estimated transformations from their groundtruth counterparts. However, this assumption is questionable as the group of underlying transformations often reside on a curved manifold rather staying in the flat Euclidean space. For this reason, we should use the geodesic to characterize how an image transform along the manifold of a Lie group, and adopt its length to measure the loss between two transformations. Particularly, we present to autoencode the homography Lie group PG(2) that contains a rich family of spatial transformations to learn image representations. Moreover, we make an estimate of the intractable Riemannian logarithm by projecting PG(2) to a subgroup of rotation transformations SO (3)$ that allows the matrix logarithm. Experiments demonstrate the proposed AETv2 model greatly outperforms its previous version as well as the other state-of-the-art self-supervised models in multiple representation learning tasks.
Formulation

Figure 1: The deviation between two transformations should be measured along the curved manifold (Lie group) of transformations rather than through the forbidden Euclidean space of transformations.
Unlike the first
AET [1], the AETv2 is a self-trained model by minimizing the geodesic distance between
two transformations, since a transformation continuously evolves to another
transformation along the manifold of transformations rather than through the
forbidden Euclidean space of transformations as shown in Figure 1.
For this purpose,
we propose to train the AETv2 in the Lie group of transformations, by
minimizing the following geodesic distance between the grountruth
through the Riemannian logarithm ![]() at the identity transformation
at the identity transformation ![]()
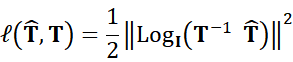
However, directly
computing the Riemannian logarithm can be intractable for many types of
transformations. For example, the
group of homography transformations does not have a
closed-form Riemannian logarithm, and we instead choose to project them into a
subgroup SO(3) of 3D rotations in homogeneous
coordinate space for images, as shown in Figure 2 below. This eventually
results in the following approximate loss defined over the projected SO(3) subgroup,
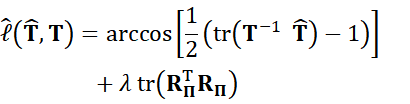
where we combine the geodesic distance of the
first term with the projection distance in the second term, and ![]() is the projection residual
is the projection residual
![]()
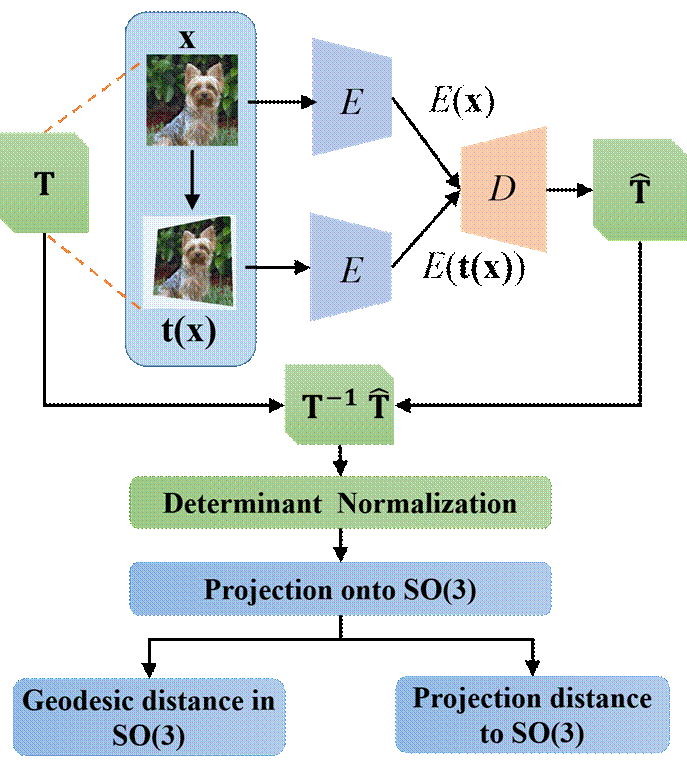
Figure 2: Illustration of how the AETv2 is
self-trained end-to- end. The output matrix ![]() from the transformation decoder is
normalized to have a unit determinant, and the projection of
from the transformation decoder is
normalized to have a unit determinant, and the projection of ![]() onto SO(3)
follows to compute the geodesic distance and the projection distance train the
model.
onto SO(3)
follows to compute the geodesic distance and the projection distance train the
model.
Results
Table 1 below reports the experiment results on CIFAR-10 with a three-layer nonlinear classifier being trained on top of the first two blocks that are pretrained by AETv2.
We also train Alexnet by AET and evaluate the performance of learned representations based on Conv4 and Conv 5 output feature maps. The proposed AETv2 can significantly close the performance gap with the fully supervised network as shown in Table 3 in the paper below.

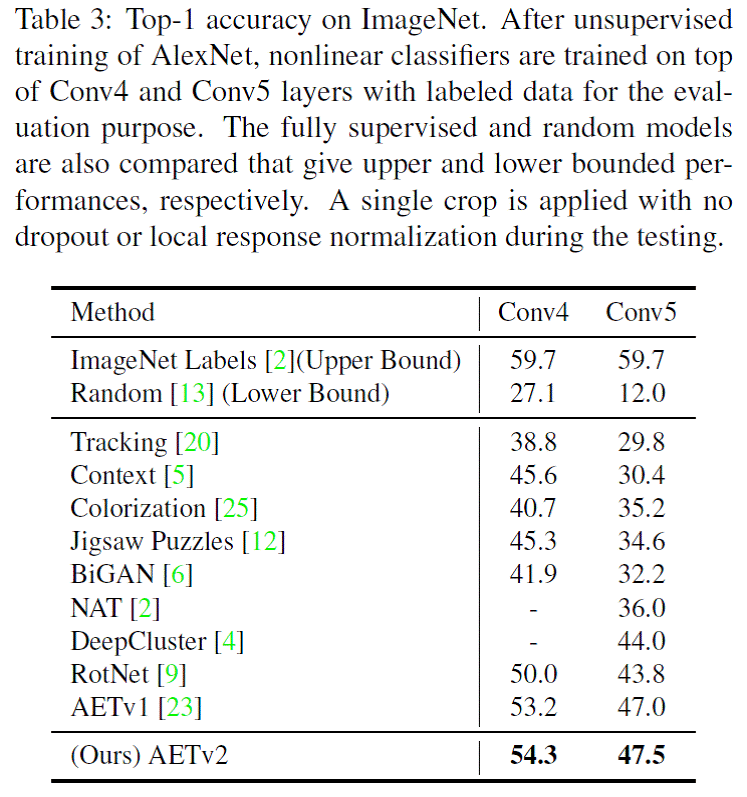
More experiment results on ImageNet and Places datasets can be found in our paper [2]. The source code will be released later.
Citation
[1] Liheng Zhang, Guo-Jun
Qi, Liqiang Wang, Jiebo
Luo. AET vs. AED: Unsupervised Representation Learning by Auto-Encoding
Transformations rather than Data, in Proceedings of IEEE Conference on Computer
Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, June 16th - June
20th, 2019. [ pdf ]
[2] Feng Lin, Haohang Xu, Houqiang Li, Haohang Xu, and Guo-Jun Qi, AETv2: AutoEncoding Transformations for Self-Supervised Representation Learning by Minimizing Geodesic Distances in Lie Groups.
November 16, 2019
© MAPLE Research