An Incomplete Map of the GAN models

Guo-Jun Qi

guojunq@gmail.com

Laboratory for MAchine Perception and LEarning (MAPLE)

 

 

In this short article, we attempt to plot an incomplete map of the GAN-family models. We focus on the training criteria of various GAN models, which are not adapted or modified with any additional features.  For this reason, the popular GANs like InfoGAN, conditional GAN and auto-encoder GANs are not within the scope of our discussion in this article. In particular, we will review a generalized GAN variant, called GLS-GAN, which unifies both Wasserstein GAN and LS-GAN that constitute the second form of regularized GAN models in literature.

 

Before we move further, let us take a glance at the map below.

 

 

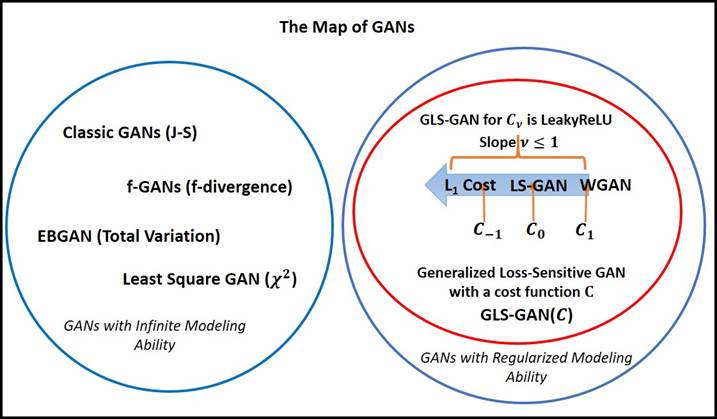
Figure: An incomplete map of GANs.

 

 

To plot this map, we need a criterion to draw the boundary between different GAN models. While there are many criteria, we classify the GANs into two large classes based on whether the model has “Regularized versus unregularized Modeling Ability” [Goodfellow2014].

 

The unregularized modeling ability (UMA), assumes that the discriminator of the GAN with UMA can distinguish between real and fake examples, no matter how these samples are distributed.  This is indeed a non-parametric assumption where the discriminator can be regressed to any arbitrary form.

 

In contrast, the GANs with regularized modeling ability (RMA) resorts to a regularized model to distinguish between real and fake examples whose distributions satisfy certain regularity conditions.  For example, both LS-GAN [Loss-Sensitive GAN, Qi2017] and WGAN [Wasserstein GAN, Arjovsky2017] are trained in a space of Lipschitz continuous functions, which are based on the Lipschitz regularity to distinguish between real and fake samples [Qi2017].

 

The significance of UMA and RMA is they are assumed explicitly or implicitly in theoretical analysis to prove the consistency conjecture of a proposed GAN model, which is the density of their generated samples match the density of true samples.

 

It has been shown [Qi2017] that both LS-GAN and WGAN are based on the Lipschitz regularity, an assumption that the model has regularized modeling ability in contrast to the non-parametric assumption of unregularized modeling ability used. 

 

Class 1: Unregularized Modeling Ability (UMA)

 

The first class of unregularized GANs contain the classic GAN [Goodfellow2014], EBGAN [Zhao2016], least-square GAN [Mao2017] and f-divergence GAN [Nowozin2016]. 

 

In [Arjovsky2017], it has been shown that the classic GAN and EBGAN attempt to minimize J-S distance and total variation distance between the generative density and the true data density, while the Least Square GAN is formulated to minimize their Pearson  divergence and the f-divergence GAN minimizes a family of f-divergence. 

 

Table: GANs with UMA and the distance between distributions they minimize to learn the generator.

GANs with UMA

Distance between distributions

The classic GAN

J-S distance

EBGAN

Total Variation

Least Square GAN

  divergence

f-GAN

f-divergence

 

 

Vanishing Gradient: What is interesting is these unregularized modeling ability GANs all suffer from the vanishing gradient problem as discussed in [Arjovsky2015].

If the manifold of real data and the manifold of generated data has no or negligible overlap, the distances they are posed to minimize will become a constant causing vanishing gradient that cannot update the generator at all. This is a problem that has been reported in [Goodfellow2013] since the first GAN (J-S) was proposed.

 

Intractable Sample Complexity: It is particularly worth noting that the unregularized GANs usually require an intractable number of training samples to reach a satisfactory accuracy in generating samples indistinguishable from real ones [Arora2017, Qi2017]. In other words, this implies unregularized GANs could be easily overfit to memorize existing samples rather than generalize to produce new samples, the most sought property we expect over the GAN models.  This inspires us to pursue an alternative class of regularized GAN models that are more competent in generalization.

 

Open Question: Is this only a coincidence between unregularized GANs and vanishing gradient problem?  In other words, does the unregularity inevitably cause vanishing gradient? Can we find some GANs with UMA but can avoid the vanishing gradient problem? Probably.

 

Class 2: Regularized Modeling Ability (RMA)

 

On the contrary, the second class of GANs contain the WGAN and LS-GAN recently developed.  By chance, both models are built based on Lipschitz regularities [Qi2017], and they do not need unregularzied modeling ability to prove the consistency conjecture.

 

Even more, in [Qi2017], it is shown that both WGAN and LS-GAN belong to a super class of Generalized LS-GAN (GLS-GAN):

                1. WGAN is the GLS-GAN with a cost of  ,

                2. LS-GAN is the GLS-GAN with a cost of .

More GLS-GANs can be found by defining a proper cost function satisfying some conditions [Qi2017]. 

An interesting example is when , it will define a GLS-GAN with a L1 cost that minimizes the difference between the loss functions of real and generated samples (up to their margin). This is quite different from the idea behind both LS-GAN and WGAN, but preliminary results show that it works!

For details, please refer to Appendix D of [Qi2017].

 

Obviously, there should exist the other GANs with RMA, but not belonging to the GLS-GAN.  More research efforts deserve to discover more GANs with RMA that can properly regularize the data generation process by introducing priors characterizing the true data distribution beyond the Lipschitz assumptions. This should be an interesting direction to expand the territory of the GANs.

   

Examples of GLS-GAN (Generalized LS-GAN)

 

We can adopt a cost function of Leaky Linear Rectifier  to define the GLS-GAN with a slope .  Then WGAN is GLS-GAN with   and LS-GAN is GLS-GAN with .

 

Results on Generalization Performances

 

To compare the generalization performance among different GANs, we propose a new metric called Minimum Reconstruction Error (MRE). The idea is to split dataset into three parts: training, validation and test.  We use training set to train different GANs, and tune their hyperparameters (including learning rate, when to stop training iterations) on a validation set.  Then on the test set, for a given sample x, we aim to find an optimal z that can reconstruct x as much as possible. That is done by defining 

Clearly, if the generator G is adequate to produce new samples, it should have a small reconstruction error on generating unseen examples on a separate test set. Our experiment results on CIFAR-10 and tiny ImageNet show that regularized models outperform the unregularized GAN in MRE. 

 

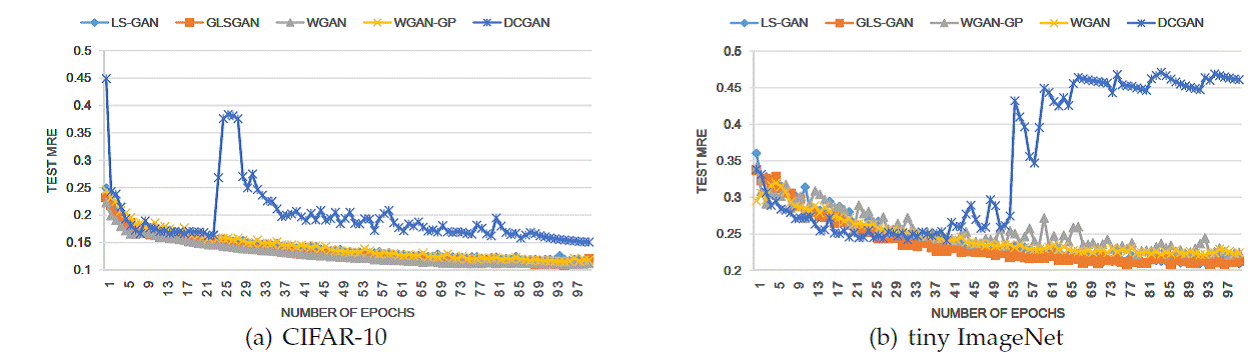
Figure: The change of test MREs on CIFAR-10 and tiny ImageNet over epochs.

 

Moreover, as illustrated below, among regularized GANs, the GLS-GAN has the smallest MRE. This is not a surprising result, since these regularized GANs, including LS-GAN, WGAN and WGAN-GP, are only special cases of GLS-GAN. More results can be found in [Qi2017].

                            

Figure: The images reconstructed by various GANs on CIFAR-10 with their MREs on the test set in parentheses.

 

Figure: The images reconstructed by various GANs on tiny ImageNet with their MREs on the test set in parentheses.

 

 

Source Codes

We have implemented the GLS-GAN in both pytorch, and tensorflow at our lab github homepage https://github.com/maple-research-lab .

Pytorch version: https://github.com/maple-research-lab/glsgan-gp

Tensorflow version: https://github.com/maple-research-lab/lsgan-gp-alt

Original Torch version: https://github.com/maple-research-lab/glsgan

In the GLS-GAN, we can run both LS-GAN and WGAN as its special cases. More details about GLS-GAN can be found at [Qi2017].

 

References

[Qi2017] G.-J. Qi, Loss-Sensitive Generative Adversarial Networks, preprint, 2017.

[Goodfellow2013] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Qzair, A. Courville and Y. Bengio, Generativ Adversarial Nets, in Advances in Neural Information Processing Systems, 2014, pp. 2672-2680.

[Arjovsky2015] M. Arjovsky and L. Bottou. Towards Principled Methods for Training Generative Adversarial Networks, 2015.

[Nowozin2016] S. Nowozin, B. Cseke, and R. Tomioka, f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization, 2016.

[Arjovsky2017] M. Arjovsky, S. Chintala, and L. Bottou. Wasserstein GAN, 2017.

[Zhao2016] J. Zhao, M. Mathieu, and Y. LeCun, Energy-based Generative Adversarial Network, 2016.

[Mao2017] X. Mao, Q. Li, H. Xie, R. Y.K. Lau and Z. Wang, Least Squares Generative Adversarial Networks, 2017.

[Arora2017] S. Arora, R. Ge, Y. Liang, T. Ma and Y. Zhang, Generalization and Equilibrium in Generative Adversarial Nets, 2017.

 

Updated on March 4th 2018

©MAPLE Research