AVT: Unsuperivised Learning of Transformation Equivariant Representations by Autoencoding Variational Transformations

Guo-Jun Qi

Laboratory for MAchine Perception and LEarning (MAPLE)

Abstract: The learning of Transformation-Equivariant Representations (TERs), which is introduced by Hinton et al., has been considered as a principle to reveal visual structures under various transformations. It contains the celebrated Convolutional Neural Networks (CNNs) as a special case that only equivary to the translations. In contrast, we seek to train TERs for a generic class of transformations and train them in an unsupervised fashion. To this end, we present a novel principled method by Autoencoding Variational Transformations (AVT), compared with the conventional approach to autoencoding data. Formally, given transformed images, the AVT seeks to train the networks by maximizing the mutual information between the transformations and representations. This ensures the resultant TERs of individual images contain the intrinsic information about their visual structures that would equivary extricably under various transformations. Technically, we show that the resultant optimization problem can be efficiently solved by maximizing a variational lower-bound of the mutual information. This variational approach introduces a transformation decoder to approximate the intractable posterior of transformations, resulting in an autoencoding architecture with a pair of the representation encoder and the transformation decoder. Experiments demonstrate the proposed AVT model sets a new record for the performances on unsupervised tasks, greatly closing the performance gap to the supervised models.

Transformation Equivariant Representations

In a general sense, a Transformation Equivariant Representation (TER) is supposed to contain sufficient information about the visual structures of an individual image such that a transformation can be predicted from the representations of an original and transformed image. The criterion of learning a TER has been explored to train a new paradigm of Auto-Encoding Transformation (AET) [2] rather than data like in the conventional auto-encoders (see http://maple-lab.net/projects/AET.htm for more information about AET). In contrast, the proposed AVT seeks to directly maximize the mutual information between the representation and transformation. This provides an information-theoretical perspective to train the TER in a more principled fashion, as well as reveals a direct connection between the learned representation and the applied transformation.

The transformation equivariance is an important property to explore in training the representations, because

1. It enforces the representation to encode the most essential visual structures of images so that the transformation can be decoded from representations before and after the transformation.

2. Compared with the conventional auto-encoder that attempts to reconstruct the input image in a high-dimensional signal space, decoding transformations is easier since a transformation often resides in a lower dimensional space with much fewer degree of freedom. This presents the learned representations from over-representing images with unnecessary details, and thus provides more compact features only encoding the most intrinsic structures that equivary to extrinsic transformations.

Formulations

Given a sample x randomly drawn from the data distribution p(x), the AVT seeks to learn its representation z by maximizing the expected mutual information over p(x)

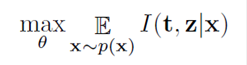
While it is hard to directly maximize the above mutual information, a variational lower bound is derived that is tractably maximize:

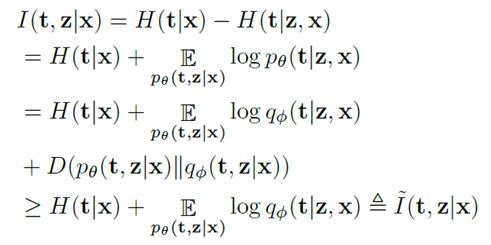
where q(t,z|x) is the transformation decoder and p(t,z|x) is the TER encoder.

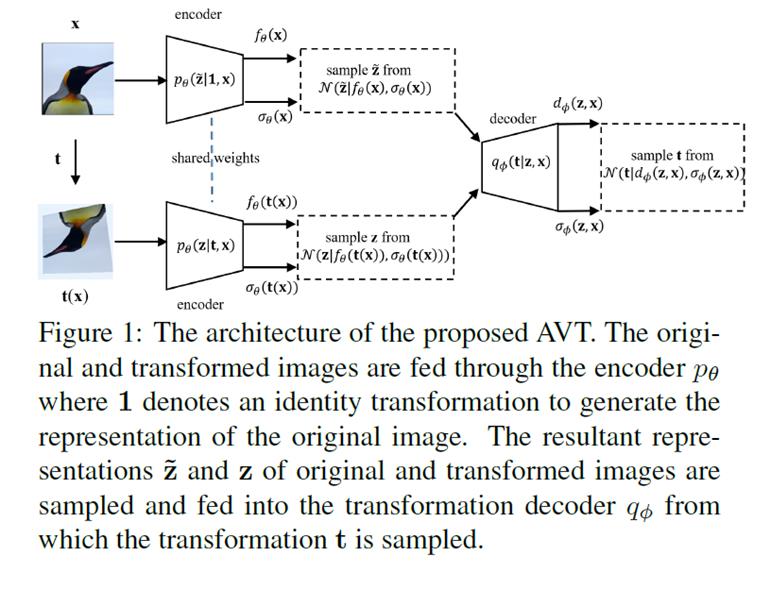
Figure 1 illustrates the architecture of the proposed AVT. For more details about how to train AVT, please refer to [2].

Experiments

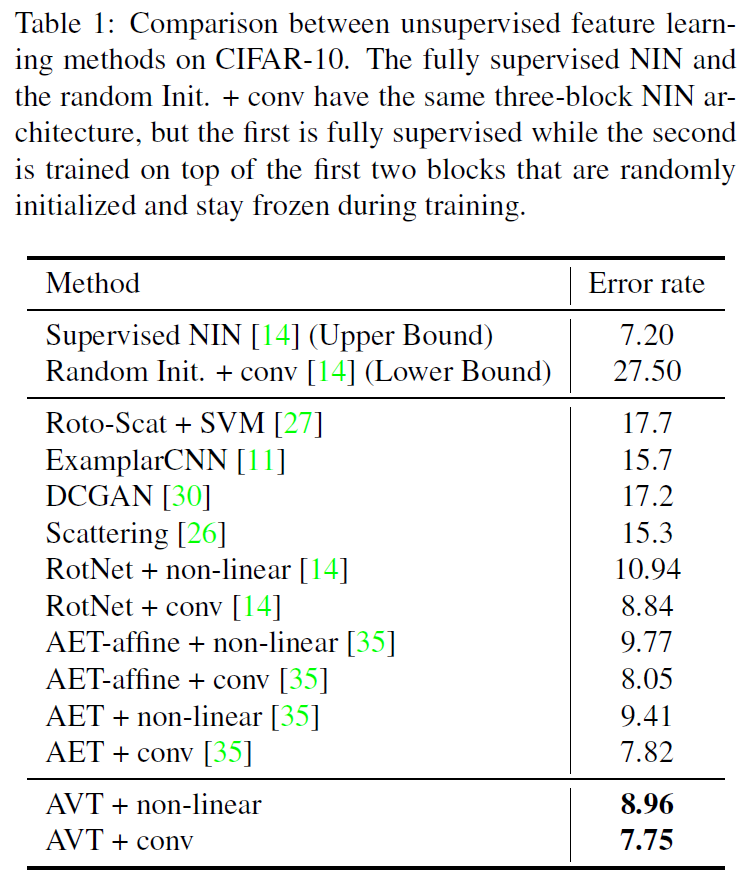
Our results on CIFAR-10 in Table 1 show the AVT outperforms the other compared unsupervised models.

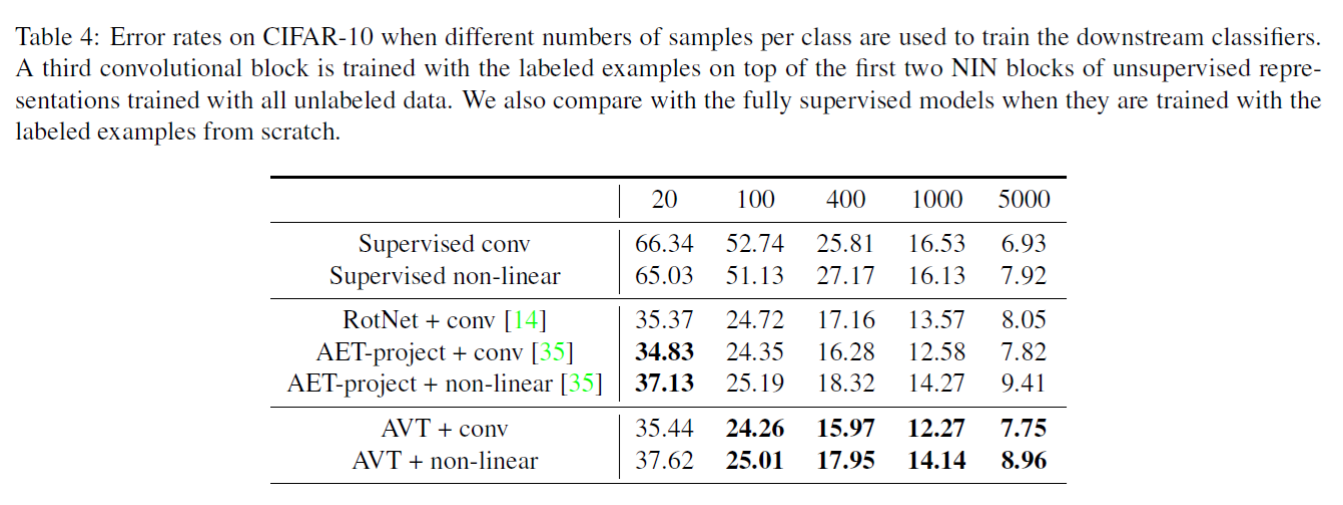
Moreover, Table 4 shows with few number of samples per class used to train the downstream classifiers, the AVT paradigms still achieve very competitive accuracies compared with the other methods.

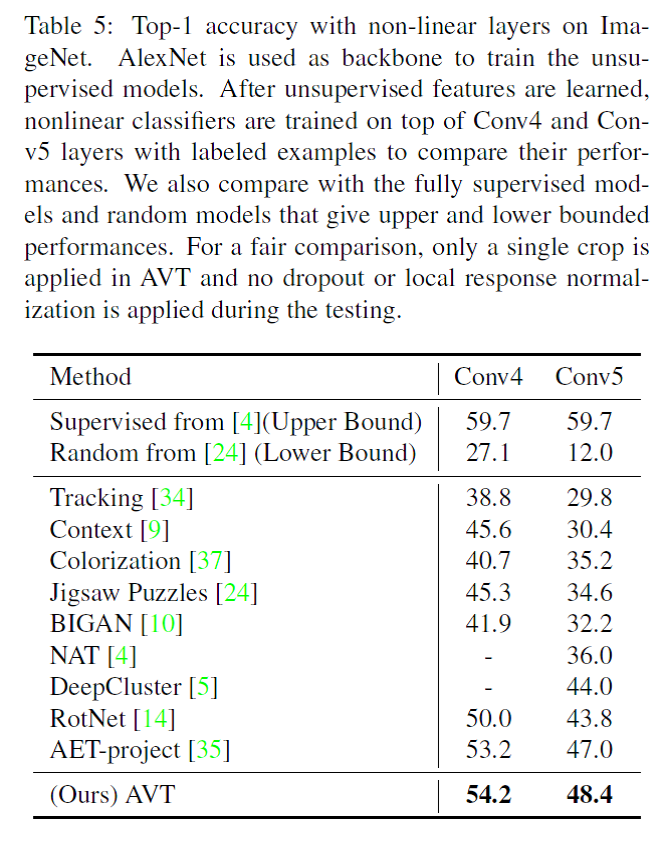
The results on ImageNet in Table 5 also demonstrate the AVT can greatly close the performance gap with the fully supervised models (54.2% vs. 59.7% with Conv4 representation and 48.4% vs. 59.7% with Conv5 representation).

More results can be found in [2].

References

[1] Liheng Zhang, Guo-Jun Qi, Liqiang Wang, Jiebo Luo. AET vs. AED: Unsupervised Representation Learning by Auto-Encoding Transformations rather than Data, in Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, June 16th - June 20th, 2019. [pdf]

[2] Guo-Jun Qi, Liheng Zhang, Chang Wen Chen, Qi Tian. AVT: Unsupervised Learning of Transformation Equivariant Representations by Autoencoding Variational Transformations, arXiv:1903.10863 [pdf]

March 27, 2019